Opäť tu máme nedeľný retro článok s obľúbeným matematickým orieškom.

Mandelbrotova množina, alebo, ako zamestnať osobný mikropočítač

Keď sa matematik Gaston Julia (1893–1978) zaoberal problémami zostrojovania fraktálnych (zlomkových) kriviek, iste netušil ich veľkú budúcnosť. Výsledky jeho práce sa používajú v počítačovej grafike pri vytváraní vierohodných obrázkov horských chrbtov či morských pobreží. Jeho nasledovník bol výskumník firmy IBM – Benoit Mandelbrot. Našiel v rovine komplexných čísel zaujímavú množinu. Dnes nesie jeho meno – Mandelbrotova množina.

Povedzme si o nej niečo viac. Každé komplexné číslo z možno zobraziť ako bod komplexnej roviny. Súradnica bodu na osi x je určená reálnou časťou a súradnica na osi y imaginárnou časťou komplexného čísla. Počítajme hodnotu výrazu zn = z(n-1)^2  + u[mi]. Zn je premenná s počiatočnou hodnotou z0 = u[mi] a u[mi] je komplexná konštanta. Nech napríklad z0 = u[mi] = 1 + 2i. Prvé tri kroky výpočtu dajú výsledky:
z1=-2 +6i
z2 =-31 – 22i
z3=-374 + 684i
Pozrime sa na absolútnu hodnotu výsledkov Zn. Musíme sčítať štvorce ich reálnej a imaginárnej časti a celkový súčet odmocniť. Absolutne hodnoty sú 6,325; 38,013; 1 445,33. Vidíme, že rýchlo rastú. Čísla u[mi] s takouto vlastnosťou nie sú pre nás zaujímavé.

Mandelbrotova množina je množina takých komplexných čísel u[mi], pre ktoré veľkosť |zn| ostáva konečná aj po l’ubovolnom počte krokov nášho výpočtu. V teórii sa hovorí, že naše komplexné číslo |zn| uteká do nekonečna práve vtedy, ak po istom počte krokov dosiahne jeho absolútna hodnota veľkosť 2 a viac. Pri výpočtoch sa ukazuje, že dostatočne veľa utekajúcich bodov dosiahne hodnotu 2 už po niekoľkých krokoch. Pri voľbe rozumného počtu krokov k, všetky body u na komplexnej rovine, pre ktoré platí |zk| < 2, patria do Mandelbrotovej množiny. Obvykle sa udávajú potrebné počty krokov k rádovo v stovkách.

Popíšme si postup, ktorý nám umožní vidieť Mandelbrotovu množinu a jej okolie na farebnom monitore mikropočítača. Najprv si vyberieme štvorcovú alebo obdlžnikovú oblasť komplexnej roviny, ktorú chceme zviditeľniť. Určíme jej súradnice na reálnej osi XD, XH a na imaginárnej osi YD, YH. Rozmery matice šachovnicovo rozmiestnených obrazových bodov (ďalej ich budeme nazývať pixelmi) musíme prispôsobiť možnostiam nášho mikropočítača. Snažíme sa plne využiť kapacitu obrazovej pamäti. Rozmery strán každého pixelu DX, DY vypočítame tak, že dlžku x-ovej (y-ovej) súradnice strán oblasti podelíme počtom stlpcov (riadkov) obrazu. Zvolený počet krokov pre získanie Mandelbrotovej množiny označíme KH.
Teraz nasleduje jadro postupu, ktorý je uvedený pre pixel v M-tom riadku a N-tom stĺpci. Algoritmus má štyri časti. Treba ho opakovať pre každý pixel.

1. Vypočítame reálnu čast čísla zodpovedajúcu danému pixelu ako N-DX + XD a jeho imaginárnu časť ako M-DY+YD.
2. Vložíme počiatočné hodnoty premennej z a premennej uchovávajúcej počet vykonaných opakovaní k na: zo = u[mi] a k0 = 0
3. Pokiaľ k nedosiahne hodnotu väčšiu alebo rovnú KH, alebo nezávisle na tom |z| nie je väčšia alebo rovná 2, vykonáme nasledujúce operácie: z <- z^2 + u[mi]; k <- k+1
4. Určime farbu pixelu v M-tom riadku a N-tom stlpci podla hodnoty, ktorú dosiahla premenná k v tretej časti algoritmu.

Ak sa k = kH, nech je pixel čierny. Tieto pixely tvoria samotnú Mandelbrotovu – množinu. V ostatných prípadoch je možné pixel vysvietiť farbou podľa našich estetických zámerov a podľa počtu farieb, ktorým disponujeme. Môžeme zvoliť napríklad taký postup, aby sa každá farba vyskytovala v obrázku iba raz, alebo naopak, aby každá zmena k o jednotku zmenila farbu pixelov. Okolie čiernej Mandelbrotovej množiny bude hýriť farbami. Ak sú naše zobrazovacie možnosti iba čiernobiele, pri k rovnom kH pixel nech je čierny, v ostatných prípadoch nech je biely.

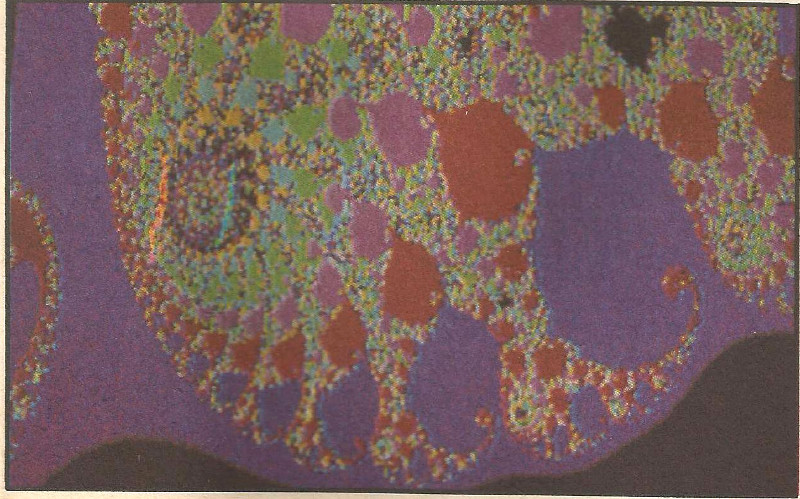
Pri podrobnejšom pohľade na získané obrázky vidíme, že materská množina má na krajoch prilepené množstvo menších výčnelkov pripomínajúcich bradavice. Všetky čierne oblasti sú spojené aspoň tenkými prielivmi. Možno totiž dokázať, že Mendelbrotova množina je spojitá.

Samotný program je jednoduchý, ale vzhľadom na obrovský počet pixelov a veľký počet opakovaní trvajú výpočty pomerne dlho. Na mikropočítači PP01 trvá výpočet obrázku rozmerov 256 X 256 pixelov, hodnote kH=100 a programe v BASICU viac ako 12 hodín. Možno síce znížiť počet pixelov i opakovaní, ale zaplatíme za to zníženou jemnosťou obrázku. Pri dlhom čakaní na výsledok l’ahko pochopíme, prečo je Mandelbrotova množina obľúbeným testom rýchlosti pre paralelne pracujúce počítače. Napriklad OMS T 414 zvládne obrázok 512 X 512 pixelov pri 256 krokoch rádovo za desatiny sekundy…
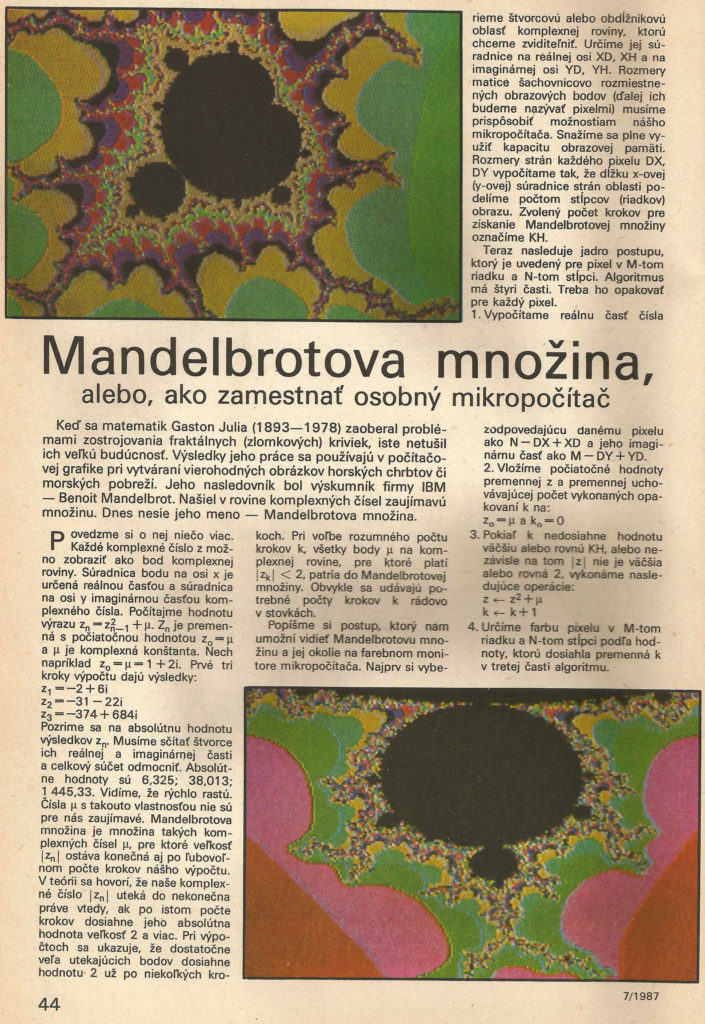
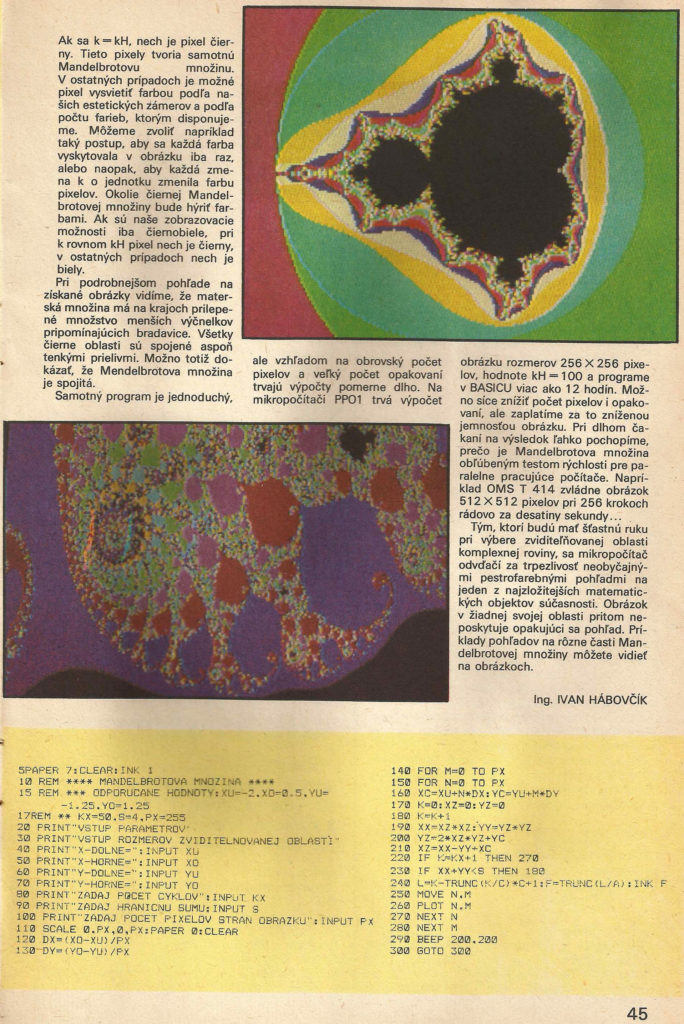
Tým, ktorí budú mať šťastnú ruku pri výbere zviditeľňovanej oblasti komplexnej roviny, sa mikropočítač odvďačí za trpezlivosť neobyčajnými pestrofarebnými pohľadmi na jeden z najzložitejších matematických objektov súčasnosti. Obrázok v žiadnej svojej oblasti pritom neposkytuje opakujúci sa pohľad. Príklady pohľadov na rôzne časti Mandelbrotovej množiny môžete vidieť na obrázkoch.

Ing. IVAN HÁBOVČÍK

Elektrón 7 / 1987, strana 44 a 45

5 PAPER 7: CLEAR: INK 1
10 REM **** MANDELBROTOVA MNOZINA ****
15 REM *** ODPORUCANE HODNOTY: XU=-2,XO=0.5,YU=-1.25,YO=1.25 
17 REM ** KX=50,S=4,PX=255 
20 PRINT "VSTUP PARAMETROV"
30 PRINT "VSTUP ROZMEROV ZVIDITELNOVANEJ OBLASTI"
40 PRINT "X-DOLNE=": INPUT XU 
50 PRINT "X-HORNE=": INPUT XO
60 PRINT "Y-DOLNE=": INPUT YL
70 PRINT "Y-HORNE=": INPUT YO 
80 PRINT "ZADAJ POCET CYKLOV": INPUT KX
90 PRINT "ZADAJ HRANICNU SUMU": INPUT S
100 PRINT "ZADAJ POCET PIXELOV STRAN OBRAZKU": INPUT PX
110 SCALE 0,PX,0,PX: PAPER 0: CLEAR
120 DX=(XO-XU)/PX
130 DY=(YO-YU)/PX
140 FOR M=0 TO PX
150 FOR N=0 TO PX
160 XC=XU+N*DX: YC=YU+M*DY
170 K=0: XZ=0: YZ=0
180 K=K+1
190 XX=XZ*XZ: YY=YZ*YZ 
200 YZ=2*XZ*YZ+YC
210 XZ=XX-YY+XC
220 IF K=KX+1 THEN 270
230 IF XX+YY<S THEN 180
240 L=K-TRUNC(K/C)*C+1: F=TRUNC(L/A): INK F
250 MOVE N,M
260 PLOT N,M
270 NEXT N
280 NEXT M
290 BEEP 200,200
300 GOTO 300

---

Jedna poznámka pod čiarou k uverejnenému programu: Riadok 240 vyzerá ako z „iného sveta“. Premenné C a A nie sú pred použitím definované, rovnako ani F, takže samozrejme to nemôže fungovať. Ak máte predstavu ako to má správne vyzerať podeľte sa o ňu, prosím, v komentári. Vďaka.

/ikon